JEE Mains Jan 30, 2023 Shift 2 Questions with solutions

Question 1

The

\mathrm{Cl}-\mathrm{Co}-\mathrm{Cl}

bond angle values in a fac-

\left[\mathrm{Co}\left(\mathrm{NH}_{3}\right)_{3} \mathrm{Cl}_{3}\right]

complex is/are :

Options:

A)

90^{\circ} ~\&~ 120^{\circ}

B)

90^{\circ}

C)

180^{\circ}

D)

90^{\circ} ~\& ~180^{\circ}

Question 2

Bond dissociation energy of "E-H" bond of the "

\mathrm{H}_{2} \mathrm{E}

" hydrides of group 16 elements (given below), follows order.

A.

\mathrm{O}

B.

\mathrm{S}

C. Se

D.

\mathrm{Te}

Choose the correct from the options given below:

Options:

A)

\mathrm{A}>\mathrm{B}>\mathrm{C}>\mathrm{D}

B)

\mathrm{D}>\mathrm{C}>\mathrm{B}>\mathrm{A}

C)

\mathrm{B}>\mathrm{A}>\mathrm{C}>\mathrm{D}

D)

\mathrm{A}>\mathrm{B}>\mathrm{D}>\mathrm{C}

Numerical TypeQuestion 3

A short peptide on complete hydrolysis produces 3 moles of glycine (G), two moles of leucine (L) and two moles of valine (V) per mole of peptide. The number of peptide linkages in it are ________.

Question 4

Formulae for Nessler's reagent is :

Options:

A)

\mathrm{KHgI}_3

B)

\mathrm{HgI}_2

C)

\mathrm{KHg}_2 \mathrm{I}_2

D)

\mathrm{K}_2 \mathrm{HgI}_4

Question 5

Match List I with List II:

List I (Complexes)		List II (Hybridisation)
A.	$\left[\mathrm{Ni}(\mathrm{CO})_{4}\right]$	I.	$\mathrm{sp}^{3}$
B.	$\left[\mathrm{Cu}\left(\mathrm{NH}_{3}\right)_{4}\right]^{2+}$	II.	dsp $^{2}$
C.	$\left[\mathrm{Fe}\left(\mathrm{NH}_{3}\right)_{6}\right]^{2+}$	III.	$\mathrm{sp}^{3}\mathrm{d}^{2}$
D.	$\left[\mathrm{Fe}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+}$	IV.	$\mathrm{d}^{2} \mathrm{sp}^{3}$

Options:

A)

A-I, B-II, C-III, D-IV

B)

A-II, B-I, C-III, D-IV

C)

A-I, B-II, C-IV, D-III

D)

A-II, B-I, C-IV, D-III

Question 6

\mathrm{KMnO}_4

oxidises

\mathrm{I}^{-}

in acidic and neutral/faintly alkaline solutions, respectively, to :

Options:

A)

\mathrm{IO}_3^{-} ~\&~ \mathrm{IO}_3^{-}

B)

\mathrm{I}_2 ~\&~ \mathrm{I}_2

C)

\mathrm{I}_2 ~\&~ \mathrm{IO}_3^{-}

D)

\mathrm{IO}_3^{-} ~\&~ \mathrm{I}_2

Question 7

The correct order of

\mathrm{pK}_{\mathrm{a}}

values for the following compounds is:

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Alcohols, Phenols and Ethers Question 37 English

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Alcohols, Phenols and Ethers Question 37 English

Options:

A)

\mathrm{a}>\mathrm{b}>\mathrm{c}>\mathrm{d}

B)

c > a > d > b

C)

\mathrm{b}>\mathrm{d}>\mathrm{a}>\mathrm{c}

D)

b > a > d > c

Question 8

The wave function

(\Psi)

of

2 \mathrm{~s}

is given by

\Psi_{2 \mathrm{~s}}=\frac{1}{2 \sqrt{2 \pi}}\left(\frac{1}{a_0}\right)^{1 / 2}\left(2-\frac{r}{a_0}\right) e^{-r / 2 a_0}

At

r=r_0

, radial node is formed. Thus,

r_0

in terms of

a_0

Options:

A)

r_0=a_0

B)

r_0=4 a_0

C)

r_0=2 a_0

D)

r_0=\frac{a_0}{2}

Numerical TypeQuestion 9

The strength of 50 volume solution of hydrogen peroxide is ______ $\mathrm{g} / \mathrm{L}$ (Nearest integer).

Given:

Molar mass of

\mathrm{H}_{2} \mathrm{O}_{2}

is

34 \mathrm{~g} \mathrm{~mol}^{-1}

Molar volume of gas at

\mathrm{STP}=22.7 \mathrm{~L}

Numerical TypeQuestion 10

1 mole of ideal gas is allowed to expand reversibly and adiabatically from a temperature of

27^{\circ} \mathrm{C}

. The work done is

3 \mathrm{~kJ} \mathrm{~mol}^{-1}

. The final temperature of the gas is ________

\mathrm{K}

(Nearest integer).

Given

\mathrm{C_V}=20 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}

Question 11

Given below are two statements: One is labelled as Assertion A and the other is labelled as Reason R.

Assertion A: JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Aldehydes, Ketones and Carboxylic Acids Question 40 English 1

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Aldehydes, Ketones and Carboxylic Acids Question 40 English 1

can be easily reduced using

\mathrm{Zn}-\mathrm{Hg} / \mathrm{HCl}

to

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Aldehydes, Ketones and Carboxylic Acids Question 40 English 2

Reason

\mathrm{R}: \mathrm{Zn}-\mathrm{Hg} / \mathrm{HCl}

is used to reduce carbonyl group to

-\mathrm{CH}_{2}-

group.

In the light of the above statements, choose the correct answer from the options given below:

Options:

A)

{ \text {Both } A \text { and }} \mathrm{R}

are true and

\mathrm{R}

is the correct explanation of

\mathrm{A}

B)

\mathrm{A}

is false but

\mathrm{R}

is true

C)

A is true but

\mathrm{R}

is false

D)

Both

\mathrm{A}

and

\mathrm{R}

are true but

\mathrm{R}

is not the correct explanation of

\mathrm{A}

Question 12

1 \mathrm{~L}, 0.02 \mathrm{M}

solution of

\left[\mathrm{Co}\left(\mathrm{NH}_{3}\right)_{5} \mathrm{SO}_{4}\right]

Br is mixed with

1 \mathrm{~L}, 0.02 \mathrm{M}

solution of

\left[\mathrm{Co}\left(\mathrm{NH}_{3}\right)_{5} \mathrm{Br}\right] \mathrm{SO}_{4}

. The resulting solution is divided into two equal parts

(\mathrm{X})

and treated with excess of

\mathrm{AgNO}_{3}

solution and

\mathrm{BaCl}_{2}

solution respectively as shown below:

1 \mathrm{~L}

Solution

(\mathrm{X})+\mathrm{AgNO}_{3}

solution (excess)

\longrightarrow \mathrm{Y}

1 \mathrm{~L}

Solution

(\mathrm{X})+\mathrm{BaCl}_{2}

solution (excess)

\longrightarrow \mathrm{Z}

The number of moles of

\mathrm{Y}

and

\mathrm{Z}

respectively are

Options:

A)

0 .01,0.01

B)

0.01,0.02

C)

0.02,0.01

D)

0.02,0.02

Numerical TypeQuestion 13

An organic compound undergoes first-order decomposition. If the time taken for the

60 \%

decomposition is

540 \mathrm{~s}

, then the time required for

90 \%

decomposition will be ________ s. (Nearest integer).

Given:

\ln 10=2.3 ; \log 2=0.3

Numerical TypeQuestion 14

The electrode potential of the following half cell at

298 \mathrm{~K}

\mathrm{X}\left|\mathrm{X}^{2+}(0.001 \mathrm{M}) \| \mathrm{Y}^{2+}(0.01 \mathrm{M})\right| \mathrm{Y}

is _______

\times 10^{-2} \mathrm{~V}

(Nearest integer)

Given:

\mathrm{E}^{0} _ {\mathrm{X}^{2+} \mid \mathrm{X}}=-2.36 \mathrm{~V}

\mathrm{E}_{\mathrm{Y}^{2+} \mid \mathrm{Y}}^{0}=+0.36 \mathrm{~V}

\frac{2.303 \mathrm{RT}}{\mathrm{F}}=0.06 \mathrm{~V}

Question 15

The most stable carbocation for the following is:

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Compounds Containing Nitrogen Question 40 English

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Compounds Containing Nitrogen Question 40 English

Options:

A)

b

B)

d

C)

c

D)

a

Question 16

Decreasing order towards SN 1 reaction for the following compounds is:

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Haloalkanes and Haloarenes Question 31 English

Options:

A)

a>c>d>b

B)

\mathrm{d}>\mathrm{b}>\mathrm{c}>\mathrm{a}

C)

a>b>c>d

D)

\mathrm{b}>\mathrm{d}>\mathrm{c}>\mathrm{a}

Question 17

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Compounds Containing Nitrogen Question 39 English

In the above conversion of compound $(\mathrm{X})$ to product $(\mathrm{Y})$ , the sequence of reagents to be used will be:

Options:

A)

\begin{array}{lll}\text { (i) } \mathrm{Br}_2, \mathrm{Fe} & \text { (ii) } \mathrm{Fe}, \mathrm{H}^{+} & \text {(iii) } \mathrm{LiAIH}_4\end{array}

B)

\begin{array}{lll}\text { (i) } \mathrm{Br}_2(\mathrm{aq}) & \text { (ii) } \mathrm{LiAIH}_4 & \text { (iii) } \mathrm{H}_3 \mathrm{O}^{+}\end{array}

C)

(i)

\mathrm{Fe}, \mathrm{H}^{+}

(ii)

\mathrm{Br}_2

(aq) (iii)

\mathrm{HNO}_2

(iv)

\mathrm{H}_3 \mathrm{PO}_2

D)

(i)

\mathrm{Fe}, \mathrm{H}^{+}

(ii)

\mathrm{Br}_2(\mathrm{aq})

(iii)

\mathrm{HNO}_2

(iv)

\mathrm{CuBr}

Question 18

Match List I with List II:

List I (Mixture)		List II (Separation Technique)
A.	$\mathrm{CHCl}_3+\mathrm{C}_6 \mathrm{H}_5 \mathrm{NH}_2$	I.	Steam distillation
B.	$\mathrm{C}_6 \mathrm{H}_{14}+\mathrm{C}_5 \mathrm{H}_{12}$	II.	Differential extraction
C.	$\mathrm{C}_6 \mathrm{H}_5 \mathrm{NH}_2+\mathrm{H}_2 \mathrm{O}$	III.	Distillation
D.	$\text { Organic compound in } \mathrm{H}_2 \mathrm{O}$	IV.	Fractional distillation

Options:

A)

A-III, B-I, C-IV, D-II

B)

A-II, B-I, C-III, D-IV

C)

A-IV, B-I, C-III, D-II

D)

A-III, B-IV, C-I, D-II

Question 19

Maximum number of electrons that can be accommodated in shell with

n=4

are:

Options:

A)

50

B)

32

C)

72

D)

16

Numerical TypeQuestion 20

Number of compounds from the following which will not dissolve in cold $\mathrm{NaHCO}_{3}$ and $\mathrm{NaOH}$ solutions but will dissolve in hot $\mathrm{NaOH}$ solution is ________.

JEE Main 2023 (Online) 30th January Evening Shift Chemistry - Aldehydes, Ketones and Carboxylic Acids Question 39 English

Question 21

Let

\vec{a}

and

\vec{b}

be two vectors, Let

|\vec{a}|=1,|\vec{b}|=4

and

\vec{a} \cdot \vec{b}=2

. If

\vec{c}=(2 \vec{a} \times \vec{b})-3 \vec{b}

, then the value of

\vec{b} \cdot \vec{c}

is :

Options:

A)

-48

B)

-60

C)

-84

D)

-24

Numerical TypeQuestion 22

Lead storage battery contains

38 \%

by weight solution of

\mathrm{H}_{2} \mathrm{SO}_{4}

. The van't Hoff factor is

2.67

at this concentration. The temperature in Kelvin at which the solution in the battery will freeze is ________. (Nearest integer).

Given

\mathrm{K}_{f}=1.8 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}

Question 23

Let

x=(8 \sqrt{3}+13)^{13}

and

y=(7 \sqrt{2}+9)^9

. If

[t]

denotes the greatest integer

\leq t

, then :

Options:

A)

[x]

is odd but

[y]

is even

B)

[x]

and

[y]

are both odd

C)

[x]+[y]

is even

D)

[x]

is even but

[y]

is odd

Numerical TypeQuestion 24

Let

A=\{1,2,3,5,8,9\}

. Then the number of possible functions

f: A \rightarrow A

such that

f(m \cdot n)=f(m) \cdot f(n)

for every

m, n \in A

with

m \cdot n \in A

is equal to ___________.

Numerical TypeQuestion 25

If

\int \sqrt{\sec 2 x-1} d x=\alpha \log _e\left|\cos 2 x+\beta+\sqrt{\cos 2 x\left(1+\cos \frac{1}{\beta} x\right)}\right|+

constant, then

\beta-\alpha

is equal to ____________.

Numerical TypeQuestion 26

50^{\text {th }}

root of a number

x

is 12 and

50^{\text {th }}

root of another number

y

is 18 . Then the remainder obtained on dividing

(x+y)

by 25 is ____________.

Question 27

Match List I with List II:

List I		List II
A.	Torque	I.	$\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2}$
B.	Energy density	II.	$\mathrm{kg} \,\mathrm{ms}^{-1}$
C.	Pressure gradient	III.	$\mathrm{kg}\, \mathrm{m}^{-2} \mathrm{~s}^{-2}$
D.	Impulse	IV.	$\mathrm{kg} \,\mathrm{m}^{2} \mathrm{~s}^{-2}$

Choose the correct answer from the options given below:

Options:

A)

A-IV, B-I, C-III, D-II

B)

A-IV, B-I, C-II, D-III

C)

A-I, B-IV, C-III, D-II

D)

A-IV, B-III, C-I, D-II

Question 28

A point source of

100 \mathrm{~W}

emits light with

5 \%

efficiency. At a distance of

5 \mathrm{~m}

from the source, the intensity produced by the electric field component is:

Options:

A)

\frac{1}{40 \pi} \frac{W}{m^2}

B)

\frac{1}{10 \pi} \frac{W}{m^2}

C)

\frac{1}{20 \pi} \frac{W}{m^2}

D)

\frac{1}{2 \pi} \frac{W}{m^2}

Question 29

As shown in the figure, a point charge

Q

is placed at the centre of conducting spherical shell of inner radius

a

and outer radius

b

. The electric field due to charge

\mathrm{Q}

in three different regions

\mathrm{I}, \mathrm{II}

and

\mathrm{III}

is given by:

(\mathrm{I}: r < a, \mathrm{II}: a < r < b, III: r>b )

JEE Main 2023 (Online) 30th January Evening Shift Physics - Electrostatics Question 46 English

Options:

A)

E_I=0, E_{I I}=0, E_{I I I} \neq 0

B)

E_I \neq 0, E_{I I}=0, E_{III}=0

C)

E_I \neq 0, E_{I I}=0, E_{III} \neq 0

D)

E_I=0, E_{I I}=0, E_{I I I}=0

Question 30

The output $Y$ for the inputs $A$ and $B$ of circuit is given by

JEE Main 2023 (Online) 30th January Evening Shift Physics - Semiconductor Question 32 English

Truth table of the shown circuit is:

Options:

A)

JEE Main 2023 (Online) 30th January Evening Shift Physics - Semiconductor Question 32 English Option 1

B)

JEE Main 2023 (Online) 30th January Evening Shift Physics - Semiconductor Question 32 English Option 2

C)

JEE Main 2023 (Online) 30th January Evening Shift Physics - Semiconductor Question 32 English Option 3

D)

JEE Main 2023 (Online) 30th January Evening Shift Physics - Semiconductor Question 32 English Option 4

Numerical TypeQuestion 31

A faulty thermometer reads

5^{\circ} \mathrm{C}

in melting ice and

95^{\circ} \mathrm{C}

in stream. The correct temperature on absolute scale will be __________

\mathrm{K}

when the faulty thermometer reads

41^{\circ} \mathrm{C}

.

Numerical TypeQuestion 32

As shown in figure, a cuboid lies in a region with electric field

E=2 x^{2} \hat{i}-4 y \hat{j}+6 \hat{k} \mathrm{~N} / \mathrm{C}

. The magnitude of charge within the cuboid is

n \in_{0} C

.

The value of

n

is _________ (if dimension of cuboid is

1 \times 2 \times 3 \mathrm{~m}^{3}

)

JEE Main 2023 (Online) 30th January Evening Shift Physics - Electrostatics Question 45 English

Question 33

Let

S

be the set of all values of

a_1

for which the mean deviation about the mean of 100 consecutive positive integers

a_1, a_2, a_3, \ldots ., a_{100}

is 25 . Then

S

is :

Options:

A)

\{9\}

B)

\phi

C)

\{99\}

D)

N

Question 34

Let

a, b, c>1, a^3, b^3

and

c^3

be in A.P., and

\log _a b, \log _c a

and

\log _b c

be in G.P. If the sum of first 20 terms of an A.P., whose first term is

\frac{a+4 b+c}{3}

and the common difference is

\frac{a-8 b+c}{10}

is

-444

, then

a b c

is equal to :

Options:

A)

343

B)

216

C)

\frac{343}{8}

D)

\frac{125}{8}

Question 35

If the functions

f(x)=\frac{x^3}{3}+2 b x+\frac{a x^2}{2}

and

g(x)=\frac{x^3}{3}+a x+b x^2, a \neq 2 b

have a common extreme point, then

a+2 b+7

is equal to :

Options:

A)

6

B)

\frac{3}{2}

C)

3

D)

4

Numerical TypeQuestion 36

A bag contains six balls of different colours. Two balls are drawn in succession with replacement. The probability that both the balls are of the same colour is p. Next four balls are drawn in succession with replacement and the probability that exactly three balls are of the same colour is

q

. If

p: q=m: n

, where

m

and

n

are coprime, then

m+n

is equal to :

Question 37

A force is applied to a steel wire 'A', rigidly clamped at one end. As a result elongation in the wire is

0.2 \mathrm{~mm}

. If same force is applied to another steel wire '

\mathrm{B}

' of double the length and a diameter

2.4

times that of the wire '

\mathrm{A}

', the elongation in the wire '

\mathrm{B}

' will be (wires having uniform circular cross sections)

Options:

A)

6 .9 \times 10^{-2} \mathrm{~mm}

B)

6.06 \times 10^{-2} \mathrm{~mm}

C)

2.77 \times 10^{-2} \mathrm{~mm}

D)

3.0 \times 10^{-2} \mathrm{~mm}

Question 38

The equivalent resistance between

A

and

B

is _________.

JEE Main 2023 (Online) 30th January Evening Shift Physics - Current Electricity Question 65 English

Options:

A)

\frac{1}{2} \Omega

B)

\frac{2}{3} \Omega

C)

\frac{3}{2} \Omega

D)

\frac{1}{3} \Omega

Question 39

A thin prism $P_1$ with an angle $6^{\circ}$ and made of glass of refractive index $1.54$ is combined with another prism $P_2$ made from glass of refractive index $1.72$ to produce dispersion without average deviation. The angle of prism $P_2$ is

Options:

A)

4.5^{\circ}

B)

7.8^{\circ}

C)

1.3^{\circ}

D)

6^{\circ}

Question 40

A block of

\sqrt{3} \mathrm{~kg}

is attached to a string whose other end is attached to the wall. An unknown force

\mathrm{F}

is applied so that the string makes an angle of

30^{\circ}

with the wall. The tension

\mathrm{T}

is: (Given

\mathrm{g}=10 \mathrm{~ms}^{-2}

)

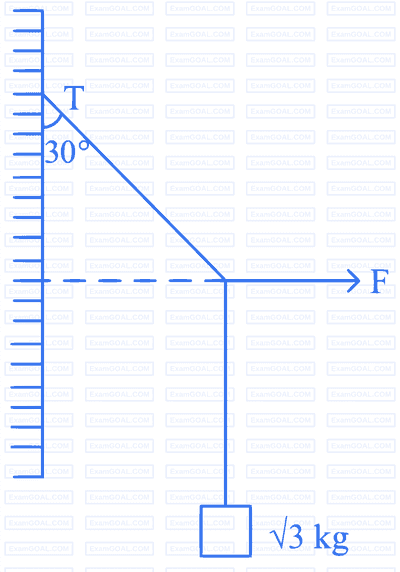
JEE Main 2023 (Online) 30th January Evening Shift Physics - Laws of Motion Question 22 English

Options:

A)

15 N

B)

10 N

C)

25 N

D)

20 N

Numerical TypeQuestion 41

In an ac generator, a rectangular coil of 100 turns each having area

14 \times 10^{-2} \mathrm{~m}^{2}

is rotated at

360 ~\mathrm{rev} / \mathrm{min}

about an axis perpendicular to a uniform magnetic field of magnitude

3.0 \mathrm{~T}

. The maximum value of the emf produced will be ________

V

.

\left(\right.

Take

\left.\pi=\frac{22}{7}\right)

Numerical TypeQuestion 42

The velocity of a particle executing SHM varies with displacement

(x)

as

4 v^{2}=50-x^{2}

. The time period of oscillations is

\frac{x}{7} s

. The value of

x

is ___________.

\left(\right.

Take

\left.\pi=\frac{22}{7}\right)

Numerical TypeQuestion 43

Consider the following equation:

2 \mathrm{SO}_{2}(g)+\mathrm{O}_{2}(g) \rightleftharpoons 2 \mathrm{SO}_{3}(g), \Delta H=-190 \mathrm{~kJ}

The number of factors which will increase the yield of

\mathrm{SO}_{3}

at equilibrium from the following is _______.

A. Increasing temperature

B. Increasing pressure

C. Adding more

\mathrm{SO}_{2}

D. Adding more

\mathrm{O}_{2}

E. Addition of catalyst

Question 44

The number of ways of selecting two numbers

a

and

b, a \in\{2,4,6, \ldots ., 100\}

and

b \in\{1,3,5, \ldots . ., 99\}

such that 2 is the remainder when

a+b

is divided by 23 is :

Options:

A)

186

B)

54

C)

108

D)

268

Multiple CorrectQuestion 45

Let

a_{1}=1, a_{2}, a_{3}, a_{4}, \ldots .

. be consecutive natural numbers.

Then

\tan ^{-1}\left(\frac{1}{1+a_{1} a_{2}}\right)+\tan ^{-1}\left(\frac{1}{1+a_{2} a_{3}}\right)+\ldots . .+\tan ^{-1}\left(\frac{1}{1+a_{2021} a_{2022}}\right)

is equal to :

Options:

A)

\frac{\pi}{4}-\cot ^{-1}(2022)

B)

\frac{\pi}{4}-\tan ^{-1}(2022)

C)

\cot ^{-1}(2022)-\frac{\pi}{4}

D)

\tan ^{-1}(2022)-\frac{\pi}{4}

Question 46

For

\alpha, \beta \in \mathbb{R}

, suppose the system of linear equations

\begin{aligned} & x-y+z=5 \\ & 2 x+2 y+\alpha z=8 \\ & 3 x-y+4 z=\beta \end{aligned}

has infinitely many solutions. Then

\alpha

and

\beta

are the roots of :

Options:

A)

x^2+18 x+56=0

B)

x^2-10 x+16=0

C)

x^2+14 x+24=0

D)

x^2-18 x+56=0

Question 47

Let

q

be the maximum integral value of

p

in

[0,10]

for which the roots of the equation

x^2-p x+\frac{5}{4} p=0

are rational. Then the area of the region

\left\{(x, y): 0 \leq y \leq(x-q)^2, 0 \leq x \leq q\right\}

is :

Options:

A)

\frac{125}{3}

B)

243

C)

164

D)

25

Question 48

The parabolas :

a x^2+2 b x+c y=0

and

d x^2+2 e x+f y=0

intersect on the line

y=1

. If

a, b, c, d, e, f

are positive real numbers and

a, b, c

are in G.P., then :

Options:

A)

\frac{d}{a}, \frac{e}{b}, \frac{f}{c}

are in A.P.

B)

\frac{d}{a}, \frac{e}{b}, \frac{f}{c}

are in G.P.

C)

d, e, f

are in A.P.

D)

d, e, f

are in G.P.

Question 49

The range of the function

f(x)=\sqrt{3-x}+\sqrt{2+x}

is :

Options:

A)

[2 \sqrt{2}, \sqrt{11}]

B)

[\sqrt{5}, \sqrt{13}]

C)

[\sqrt{2}, \sqrt{7}]

D)

[\sqrt{5}, \sqrt{10}]

Question 50

The solution of the differential equation

\frac{d y}{d x}=-\left(\frac{x^2+3 y^2}{3 x^2+y^2}\right), y(1)=0

is :

Options:

A)

\log _e|x+y|+\frac{x y}{(x+y)^2}=0

B)

\log _e|x+y|-\frac{x y}{(x+y)^2}=0

C)

\log _e|x+y|+\frac{2 x y}{(x+y)^2}=0

D)

\log _e|x+y|-\frac{2 x y}{(x+y)^2}=0

Numerical TypeQuestion 51

The number of seven digits odd numbers, that can be formed using all the

seven digits 1, 2, 2, 2, 3, 3, 5 is ____________.

Numerical TypeQuestion 52

Let

P\left(a_1, b_1\right)

and

Q\left(a_2, b_2\right)

be two distinct points on a circle with center

C(\sqrt{2}, \sqrt{3})

. Let

\mathrm{O}

be the origin and

\mathrm{OC}

be perpendicular to both

\mathrm{CP}

and

\mathrm{CQ}

. If the area of the triangle

\mathrm{OCP}

is

\frac{\sqrt{35}}{2}

, then

a_1^2+a_2^2+b_1^2+b_2^2

is equal to :

Numerical TypeQuestion 53

Let a line

L

pass through the point

P(2,3,1)

and be parallel to the line

x+3 y-2 z-2=0=x-y+2 z

. If the distance of

L

from the point

(5,3,8)

is

\alpha

, then

3 \alpha^2

is equal to :

Question 54

An object is allowed to fall from a height

R

above the earth, where

R

is the radius of earth. Its velocity when it strikes the earth's surface, ignoring air resistance, will be

Options:

A)

\sqrt{\frac{g R}{2}}

B)

\sqrt{g R}

C)

\sqrt{2 g R}

D)

2 \sqrt{g R}

Question 55

An electron accelerated through a potential difference

V_{1}

has a de-Broglie wavelength of

\lambda

. When the potential is changed to

V_{2}

, its de-Broglie wavelength increases by

50 \%

. The value of

\left(\frac{V_{1}}{V_{2}}\right)

is equal to

Options:

A)

\frac{3}{2}

B)

4

C)

3

D)

\frac{9}{4}

Question 56

In the given circuit, rms value of current

\left(I_{\mathrm{rms}}\right)

through the resistor

R

is:

JEE Main 2023 (Online) 30th January Evening Shift Physics - Alternating Current Question 30 English

Options:

A)

2 \sqrt{2} \mathrm{~A}

B)

2 \mathrm{~A}

C)

\frac{1}{2} \mathrm{~A}

D)

20 \mathrm{~A}

Question 57

A flask contains hydrogen and oxygen in the ratio of

2: 1

by mass at temperature

27^{\circ} \mathrm{C}

. The ratio of average kinetic energy per molecule of hydrogen and oxygen respectively is:

Options:

A)

1 : 1

B)

4 : 1

C)

1 : 4

D)

2 : 1

Question 58

A current carrying rectangular loop PQRS is made of uniform wire. The length $P R=Q S=5 \mathrm{~cm}$ and $P Q=R S=100 \mathrm{~cm}$ . If ammeter current reading changes from I to $2 I$ , the ratio of magnetic forces per unit length on the wire $P Q$ due to wire $R S$ in the two cases respectively $\left(f_{P Q}^I: f_{P Q}^{2 t}\right)$ is:

JEE Main 2023 (Online) 30th January Evening Shift Physics - Magnetic Effect of Current Question 37 English

Options:

A)

1 : 4

B)

1 : 3

C)

1 : 2

D)

1 : 5

Question 59

For a simple harmonic motion in a mass spring system shown, the surface is frictionless. When the mass of the block is $1 \mathrm{~kg}$ , the angular frequency is $\omega_{1}$ . When the mass block is $2 \mathrm{~kg}$ the angular frequency is $\omega_{2}$ . The ratio $\omega_{2} / \omega_{1}$ is

JEE Main 2023 (Online) 30th January Evening Shift Physics - Simple Harmonic Motion Question 28 English

Options:

A)

1 / \sqrt{2}

B)

1 / 2

C)

2

D)

\sqrt{2}

Numerical TypeQuestion 60

A stone tied to

180 \mathrm{~cm}

long string at its end is making 28 revolutions in horizontal circle in every minute. The magnitude of acceleration of stone is

\frac{1936}{x} ms^{-2}

. The value of

x

________. (Take

\pi=\frac{22}{7}

)

Question 61

Let

f, g

and

h

be the real valued functions defined on

\mathbb{R}

as

f(x)=\left\{\begin{array}{cc}\frac{x}{|x|}, & x \neq 0 \\ 1, & x=0\end{array}\right.

g(x)=\left\{\begin{array}{cc}\frac{\sin (x+1)}{(x+1)}, & x \neq-1 \\ 1, & x=-1\end{array}\right.

and

h(x)=2[x]-f(x)

, where

[x]

is the greatest integer

\leq x

. Then the

value of

\lim\limits_{x \rightarrow 1} g(h(x-1))

is :

Options:

A)

1

B)

-1

C)

\sin (1)

D)

0

Numerical TypeQuestion 62

Let

A

be the area of the region

\left\{(x, y): y \geq x^2, y \geq(1-x)^2, y \leq 2 x(1-x)\right\}

.

Then

540 \mathrm{~A}

is equal to :

Numerical TypeQuestion 63

If the value of real number

a>0

for which

x^2-5 a x+1=0

and

x^2-a x-5=0

have a common real root is

\frac{3}{\sqrt{2 \beta}}

then

\beta

is equal to ___________.

Question 64

A vehicle travels

4 \mathrm{~km}

with speed of

3 \mathrm{~km} / \mathrm{h}

and another

4 \mathrm{~km}

with speed of

5 \mathrm{~km} / \mathrm{h}

, then its average speed is

Options:

A)

3.75 \mathrm{~km} / \mathrm{h}

B)

4.25 \mathrm{~km} / \mathrm{h}

C)

3.50 \mathrm{~km} / \mathrm{h}

D)

4.00 \mathrm{~km} / \mathrm{h}

Question 65

A machine gun of mass

10 \mathrm{~kg}

fires

20 \mathrm{~g}

bullets at the rate of 180 bullets per minute with a speed of

100 \mathrm{~m} \mathrm{~s}^{-1}

each. The recoil velocity of the gun is

Options:

A)

0.02 \mathrm{~m} / \mathrm{s}

B)

1.5 \mathrm{~m} / \mathrm{s}

C)

2.5 \mathrm{~m} / \mathrm{s}

D)

0.6 \mathrm{~m} / \mathrm{s}

Question 66

As shown in the figure, a current of $2 \mathrm{~A}$ flowing in an equilateral triangle of side $4 \sqrt{3} \mathrm{~cm}$ . The magnetic field at the centroid $\mathrm{O}$ of the triangle is

JEE Main 2023 (Online) 30th January Evening Shift Physics - Magnetic Effect of Current Question 38 English

(Neglect the effect of earth's magnetic field)

Options:

A)

4 \sqrt{3} \times 10^{-4} \mathrm{~T}

B)

4 \sqrt{3} \times 10^{-5} \mathrm{~T}

C)

3 \sqrt{3} \times 10^{-5} \mathrm{~T}

D)

\sqrt{3} \times 10^{-4} \mathrm{~T}

Numerical TypeQuestion 67

In a Young's double slit experiment, the intensities at two points, for the path differences $\frac{\lambda}{4}$ and $\frac{\lambda}{3}$ ( $\lambda$ being the wavelength of light used) are $I_{1}$ and $I_{2}$ respectively. If $I_{0}$ denotes the intensity produced by each one of the individual slits, then $\frac{I_{1}+I_{2}}{I_{0}}=$ __________.

Numerical TypeQuestion 68

If the potential difference between $\mathrm{B}$ and $\mathrm{D}$ is zero, the value of $x$ is $\frac{1}{n} \Omega$ . The value of $n$ is __________.

JEE Main 2023 (Online) 30th January Evening Shift Physics - Current Electricity Question 64 English

Numerical TypeQuestion 69

A uniform disc of mass $0.5 \mathrm{~kg}$ and radius $r$ is projected with velocity $18 \mathrm{~m} / \mathrm{s}$ at $\mathrm{t}=0$ s on a rough horizontal surface. It starts off with a purely sliding motion at $\mathrm{t}=0 \mathrm{~s}$ . After $2 \mathrm{~s}$ it acquires a purely rolling motion (see figure). The total kinetic energy of the disc after $2 \mathrm{~s}$ will be __________ $\mathrm{J}$ (given, coefficient of friction is $0.3$ and $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ).

JEE Main 2023 (Online) 30th January Evening Shift Physics - Rotational Motion Question 33 English

Numerical TypeQuestion 70

A body of mass

2 \mathrm{~kg}

is initially at rest. It starts moving unidirectionally under the influence of a source of constant power P. Its displacement in

4 \mathrm{~s}

is

\frac{1}{3} \alpha^{2} \sqrt{P} m

. The value of

\alpha

will be ______.